Part .1 Intro to UWB and TWR Ranging information
Have you ever seen a drone flying? Can you imagine the potential applications these flying machines have?
Now imagine you have a swarm of them. This opens the door to a whole new world of possibilities. Then, why is not everyone is actively using them? Well, the answer is simple: they are hard to control. Today we will focus on one specific task fundamental to controlling the swarm: Localization. More specifically, we will focus on relative localization.
Relative localization is a fundamental problem in multi-agent systems that involves determining the position and orientation of one Robot relative to another. In particular, the relative localization problem between Robots \(i\) and \(j\) refers to the challenge of estimating the relative pose (position and orientation) of Robot \(j\) with in the frame of reference of Robot \(i\), based on noisy measurements obtained from sensors on both Robots.
We have set the grounds for the problem; now, let's see how to solve it. Let me first introduce you to our platform. We will be using the Crazyflie 2.1 [1], a small quadcopter that can be equipped with a UWB module. Crazyflie 2.1 is an open-source platform allowing easy customization and experimentation, making it an ideal platform for testing new algorithms.


Crazyflie 2.1 and UWB (Loco Positioning deck) DWN1000
Now we can start discussing a solution. You probably noticed how subtly I mentioned the UWB in the previous paragraph. Well, that's because the UWB is the key to one solution to this problem. The UWB is a technology that allows ranging between the Robots. This means we can measure the distance between the Robots with more or less high accuracy.
The UWB-based relative localization algorithm consists of two main parts: communication using UWB and the two-way ranging algorithm (TWR) and a Kalman Filter. In this first post of the Serie, I'll focus on the UWB and TWR. The next ones will be focused on the Kalman Filter and the implementation of the algorithm.
Disclaimer: I will use images taken from the references I'll mention in this post. I don't own any of them.
Communication using UWB and the two-way ranging algorithm
The UWB uses the Two Way Ranging Protocol (TWR) to measure the distance between the Robots. The TWR protocol requires four message exchanges between the two devices to calculate the distance. I will describe some subtle changes to the original protocol to make it more suitable for our application. These changes are published by the authors of the paper [2].
First, the initiator (Robot \(i\)) sends a POLL message to the responder (Robot \(j\)). This is called the Time of Sending Poll (TSP)
Robot \(j\) receives the message and records the Time of Reception of the Poll (TRP). Then replies with a ANSWER message. This is called the Time of Sending Response (TSR).
Robot \(i\) receives the message and records the Time of Reception of Response (TRR). With this, Robot \(i\) composes a message FINAL in which TSP, TRR, and Time Sending Final (TSF) are included. Robot \(j\) receives the message and records the Time of Reception of Final (TRF). With all the information, Robot \(j\) can calculate the distance between Robot \(i\) and \(j\). But we also want Robot \(i\) to know the distance. For this, Robot \(j\) composes a message to send back as REPORT including TSP, TRP, TSF, and TRF. This message can contain more information as ID or measurements from its sensors. This will come in handy later.

Two Way Ranging algorithm using Ultra Wide Band (UWB).
Then ToF is calculated using the following equation:
\[ToF = \frac{T_{\mathbf{Round_1}} \times T_{\mathbf{Round_2}} - T_{\mathbf{Reply_1}} \times T_{\mathbf{Reply_2}}}{T_{\mathbf{Round_1}} + T_{\mathbf{Round_2}} + T_{\mathbf{Reply_1}} + T_{\mathbf{Reply_2}}}\]and the distance between Robots \(i\) and \(j\) is calculated using the following equation:
\[\mathbf{Distance_{ij}} = \frac{ToF \times \mathbf{LightSpeed}}{2}\]Great, now that the Robots can calculate the distance between them, the question arises: how do they distinguish between the initiator and the responder? TWR is thought to be used with stationary anchors, so the initiator is always the same. In our case, we want the Robots to be able to calculate the distance between them, so we need to make some changes to the protocol. We can add a synchronization method with an extra DYNAMIC message.
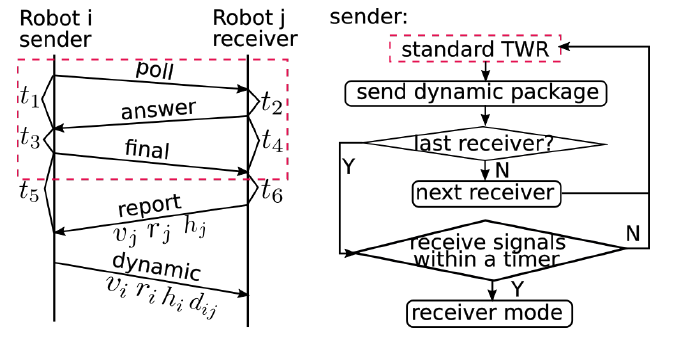
Dynamic message and Synchronisation diagram
Extra advantage, we can share sensor information from Robot \(i\) to Robot \(j\) and the distance calculated in Robot \(i\) to reduce the error in the calculation, or we can calculate once in Robot \(i\) and send it back to Robot \(j\).
We need to initialize the Protocol in all the Crazyflies (Cfs). We can decide to start with the ID 0
Initialization:
Set
current_Sender_ID= 0if
My_ID == current_Sender_ID
Set Mode = Initiatorelse
Set Mode = Responder
With that, all Cfs start listening to the same ID. We can dynamically update the ID once the Current_Sender_ID has communicated with all the receivers.
ID Update:
for
i = 0toNumber_Cfs - 1:if
My_ID == i
ContinueTWR Protocol (intitiator=
My_ID, responder=i)Swapping Protocol ( )
The implementation of the Swapping protocol can be tricky. We'll see how we can implement all this onboard the Drone in future posts. Thank you for reading the first post of this series! I'm excited to continue exploring the implementation of the Swapping protocol on board a swarm of Crazyflie Nano drones in future posts. This can be a tricky task, but I believe it's an important step to achive fast enough communication for the next steps of the project.
Stay tuned for more updates in the coming weeks.
References
[2] Shushuai Li and Mario Coppola and Christophe De Wagter and Guido C. H. E. de Croon, An autonomous swarm of micro flying Robots with range-based relative localization, 2021, 2003.05853, arXiv